Nos permite expresar en forma concisa y clara los conceptos matemáticos, de tal manera que un texto matemático que utilice el lenguaje matemático, puede ser leído por cualquier persona sin importar la lengua que hable; i.e. para un hispanoamericano, para un anglosajón, para un chino, para un japonés y para un ruso, entre otros, la expresión
significará lo mismo: "El Conjunto de los Números Racionales se define como el conjunto de los números de la forma a sobre b, tales que a y b son números enteros, con la restricción de que b es diferente de cero."
Observe como la expresión simbólica para definir al Conjunto de los Números Racionales, es mucho más concisa que la definición dada en lenguaje cotidiano, en este caso, el español.
La simbología matemática está repleta de signos o caracteres gráficos, que son como las “palabras” de un idioma. Éstas deben ser conocidas con el objeto de poder interpretar lo que se quiere decir con ellas, al tiempo que se deben utilizar para decir lo que se quiera. Cada uno de estos símbolos utilizados en matemática, son necesarios para la perfecta construcción de ideas, de manera que la sustitución de alguno de ellos por otro diferente, aunque sea gráficamente parecido, cambiaría totalmente el significado. Es decir, todas y cada una de las “palabras matemáticas” tienen un significado particular, no existiendo la posibilidad de sinónimos.
Genéricos
| Símbolo | Nombre | se lee como | Categoría |
|---|

| igualdad | igual a | todos |
| x = y significa: x e y son nombres diferentes que hacen referencia a un mismo objeto o ente. |
| 1 + 2 = 6 − 3 |
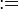

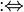
| definición | se define como | todos |
x := y o x ≡ y significa: x se define como otro nombre para y (notar, sin embargo, que ≡ puede también significar otras cosas, como congruencia)
P :⇔ Q significa: P se define como lógicamente equivalente a Q |
| cosh x := (1/2)(exp x + exp (−x)); A XOR B :⇔ (A ∨ B) ∧ ¬(A ∧ B) |
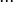

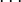


| ad infinitum o sucesión matemática | se repite/progresión | todos |
0, 1, 2, 3, ... 18 y a1, a2, a3, ...a7 y a1, a2, a3, ...an se entiende que la progresión se extiende hasta el número o valor indicado. En estos casos, 18, 7 y algún natural nrespectivamente.
1, 2, 3, 4, ... y a 1, a 2, a 3, ... y a 1, → a 2, → a 3, → ... se entiende que cada progresión se extiende infinitamente 1
2, 4, 6, 8, ... se entiende que hay un incremento progresivo según el patrón hasta el infinito.
... –4, –3, –2, –1, 0, 1, 2, 3, 4, ... se entiende que decrementa progresivamente hacia la izquierda y que aumenta progresivamente hacia la derecha, y se extiende infinitamente en ambos sentidos. |
π ≈ 3,14159265358979323846... se entiende que el valor del símbolo pi es aproximadamente 3,14159265358979323846 pero que los siguientes dígitos conocidos y desconocidos se extienden hasta el infinito2 .
 o 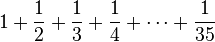 se entiende como suma de fracciones periódicas.
|
 se entiende como una matriz de progresión donde los elementos comienzan por la fila y columna de subíndice 1 y terminan en la fila de subíndice 2324, y la columna de subíndice 127. se entiende como una matriz de progresión donde los elementos comienzan por la fila y columna de subíndice 1 y terminan en la fila de subíndice 2324, y la columna de subíndice 127.
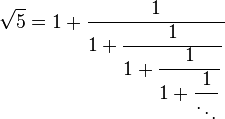 se entiende que la raíz cuadrada de 5 es igual 1 sumado la fracción de 1 sobre la repetición infinita de la misma ecuación.
|
| x = 1 + 2 + 3 + ... + 54 |
Aritmética y álgebra
| Símbolo | Nombre | se lee como | Categoría |
|---|

| adición | más | aritmética y álgebra |
| 4 + 6 = 10 significa que si a cuatro se le agrega 6, la suma, o resultado, es 10. |
| 43 + 65 = 108; 2 + 7 = 9 |

| sustracción | menos | aritmética |
| 9 − 4 = 5 significa que si 4 es restado de 9, el resultado será 5. El símbolo 'menos' también se utiliza para denotar que un número es negativo. Por ejemplo, 5 + (−3) = 2 significa que si 'cinco' y 'menos tres' son sumados, el resultado es 'dos'. |
| 87 − 36 = 51 |



| multiplicación | por | aritmética |
| 7 × 6 = 42 significa que si se cuenta siete veces seis, el resultado será 42. |
| 4 × 6 = 24 ó 4 * 6 = 24 ó 4 · 6 = 24 |
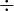
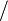

| división | entre, dividido por | aritmética |
 significa que si se hace seis pedazos uniformes de cuarenta y dos, cada pedazo será de tamaño siete. significa que si se hace seis pedazos uniformes de cuarenta y dos, cada pedazo será de tamaño siete. |
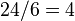 |

| sumatoria | suma sobre ... desde ... hasta ... de | aritmética |
| ∑k=1n ak significa: a1 + a2 + ... + an |
| ∑k=14 k² = 1² + 2² + 3² + 4² = 1 + 4 + 9 + 16 = 30 |

| productorio | producto sobre... desde ... hasta ... de | aritmética |
| ∏k=1n ak significa: a1a2···an |
| ∏k=14 (k + 2) = (1 + 2)(2 + 2)(3 + 2)(4 + 2) = 3 × 4 × 5 × 6 = 360 |
Lógica proposicional
| Símbolo | Nombre | se lee como | Categoría |
|---|


| implicación material o en un solo sentido | implica; si .. entonces; por lo tanto | lógica proposicional |
A ⇒ B significa: si A es verdadero entonces B es verdadero también; si B es verdadero entonces nada se dice sobre A.
→ puede significar lo mismo que ⇒, o puede ser usado para denotar funciones, como se indica más abajo. |
| x = 2 ⇒ x² = 4 es verdadera, pero 4 = x² ⇒ x = 2 es, en general, falso (ya que x podría ser −2) |


| doble implicación | si y sólo si; sii, syss3 | lógica proposicional |
| A ⇔ B significa: A es verdadera si B es verdadera y A es falsa si B es falsa. |
| x + 5 = y + 2 ⇔ x + 3 = y |

| conjunción lógica o intersección en una reja | y | lógica proposicional, teoría de rejas |
| la proposición A ∧ B es verdadera si A y B son ambas verdaderas; de otra manera es falsa. |
| n < 4 ∧ n > 2 ⇔ n = 3 cuando n es un número natural |

| disyunción lógica o unión en una reja | o, ó | lógica proposicional, teoría de rejas |
| la proposición A ∨ B es verdadera si A o B (o ambas) son verdaderas; si ambas son falsas, la proposición es falsa. |
| n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 cuando n es un número natural |

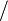
| negación lógica | no | lógica proposicional |
la proposición ¬A es verdadera si y sólo si A es falsa.
una barra puesta sobre otro operador es equivalente a un ¬ puesto a la izquierda. |
| ¬(A ∧ B) ⇔ (¬A) ∨ (¬B); x ∉ S ⇔ ¬(x ∈ S) |
Lógica de predicados
Teoría de conjuntos
| Símbolo | Nombre | se lee como | Categoría |
|---|
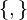
| delimitadores de conjunto | el conjunto de ... | teoría de conjuntos |
| {a,b,c} significa: el conjunto consistente de a, b, y c |
| N = {0,1,2,...} |
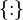

| notación constructora de conjuntos | el conjunto de los elementos ... tales que ... | teoría de conjuntos |
| {x : P(x)} significa: el conjunto de todos los x para los cuales P(x) es verdadera. {x | P(x)} es lo mismo que {x : P(x)}. |
| {n ∈ N : n² < 20} = {0,1,2,3,4} |


| conjunto vacío | conjunto vacío | teoría de conjuntos |
| {} significa: el conjunto que no tiene elementos; ∅ es la misma cosa. |
| {n ∈ N : 1 < n² < 4} = {} |


| pertenencia de conjuntos | en; está en; es elemento de; es miembro de; pertenece a | teoría de conjuntos |
| a ∈ S significa: a es elemento del conjunto S; a ∉ S significa: a no es elemento del conjunto S |
| (1/2)−1 ∈ N; 2−1 ∉ N |
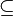

| subconjunto | es subconjunto de | teoría de conjuntos |
A ⊆ B significa: cada elemento de A es también elemento de B
A ⊂ B significa: A ⊆ B pero A ≠ B |
| A ∩ B ⊆ A; Q ⊂ R |

| unión de conjuntos | la unión de ... y ...; unión | teoría de conjuntos |
| A ∪ B significa: el conjunto que contiene todos los elementos de A y también todos aquellos de B, pero ningún otro. |
| A ⊆ B ⇔ A ∪ B = B |

| intersección de conjuntos | la intersección de ... y ...; intersección | teoría de conjuntos |
| A ∩ B significa: el conjunto que contiene todos aquellos elementos que A y B tienen en común. |
| {x ∈ R : x² = 1} ∩ N = {1} |

| diferencia de conjuntos | menos; sin | teoría de conjuntos |
| A \ B significa: el conjunto que contiene todos aquellos elementos de A que no se encuentran en B |
| {1,2,3,4} \ {3,4,5,6} = {1,2} |
Funciones
| Símbolo | Nombre | se lee como | Categoría |
|---|
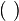
![\left[\ \right]](https://upload.wikimedia.org/math/3/a/6/3a6a4b52a2ccd7ec58002cb495362e16.png)
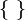
| aplicación de función; agrupamiento | de | funciones |
para aplicación de función: f(x) significa: el valor de la función f sobre el elemento x
para agrupamiento: realizar primero las operaciones dentro del paréntesis. |
| Si f(x) := x², entonces f(3) = 3² = 9; (8/4)/2 = 2/2 = 1, pero 8/(4/2) = 8/2 = 4 |

| mapeo funcional | de ... a | funciones |
| f: X → Y significa: la función f mapea el conjunto X al conjunto Y |
| Considérese la función f: Z → N definida por f(x) = x² |
 
 
| Funciones de Piso y Techo | Piso de, Techo de | funciones |
| La función piso asigna el entero más próximo por defecto, la función techo asigna el entero más próximo por exceso. |
Si x=1.5, entonces  x x =1 y =1 y  x x =2 =2 |
Números
| Símbolo | Nombre | se lee como | Categoría |
|---|

| números naturales | N | números |
| N significa: {1,2,3,...}, pero véase el artículo números naturales para una convención diferente. |
| {|a| : a ∈ Z} = N |

| números enteros | Z | números |
| Z significa: {...,−3,−2,−1,0,1,2,3,4,...} |
| {a : |a| ∈ N} = Z |

| números racionales | Q | números |
| Q significa: {p/q : p, q ∈ Z, q ≠ 0} |
| 3.14 ∈ Q; π ∉ Q |

| números reales | R | números |
| R significa: {limn→∞ an : ∀ n ∈ N: an ∈ Q, el límite existe} |
| π ∈ R; √(−1) ∉ R |

| números complejos | C | números |
| C significa: {a + bi : a, b ∈ R} |
| i = √(−1) ∈ C |

| raíz cuadrada | la raíz cuadrada de; la principal raíz cuadrada de | números reales |
| √x significa: el número positivo cuyo cuadrado es x |
| √(x²) = |x| |

| infinito | infinito | números |
| ∞ es un elemento de la recta real extendida mayor que todos los números reales; ocurre frecuentemente en límites |
| limx→0 1/|x| = ∞ |

| valor absoluto | valor absoluto de | números |
| |x| significa: la distancia en la recta real (o en el plano complejo) entre x y [[zero], se le llama también módulo] |
| |a + bi | = √(a+ b)² |
Órdenes parciales
| Símbolo | Nombre | se lee como | Categoría |
|---|

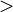
| comparación | es menor a, es mayor a | órdenes parciales |
| x < y significa: x es menor a y; x > y significa: x es mayor a y |
| 3 < 4 5 > 4 |
| Símbolo | Nombre | se lee como | Categoría |
|---|

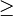
| comparación | es menor o igual a, es mayor o igual a | órdenes parciales |
| x ≤ y significa: x es menor o igual a y; x ≥ y significa: x es mayor o igual a y |
| x ≥ 1 ⇒ x² ≥ x |
Geometría euclídea
Combinatoria
Análisis funcional
Cálculo
| Símbolo | Nombre | se lee como | Categoría |
|---|
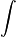
| integración | integral desde ... hasta ... de ... con respecto a ... | cálculo |
| ∫ab f(x) dx significa: el área, con signo, entre el eje-x y la gráfica de la función f entre x = a y x = b |
| ∫0b x² dx = b³/3; ∫x² dx = x³/3 |
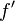
| derivación | derivada de f; f prima | cálculo |
| f '(x) es la derivada de la función f en el punto x, esto es, la pendiente de la tangente en ese lugar. |
| Si f(x) = x², entonces f '(x) = 2x y f ' '(x) = 2 |

| gradiente | del, nabla, gradiente de | cálculo |
| ∇f (x1, …, xn) es el vector de derivadas parciales (df / dx1, …, df / dxn) |
| Si f (x, y, z) = 3xy + z² entonces ∇f = (3y, 3x, 2z) |
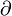
| derivada parcial | derivada parcial de | cálculo |
| Con f (x1, …, xn), ∂f/∂xi es la derivada de f con respecto a xi, con todas las otras variables mantenidas constantes. |
| Si f(x, y) = x²y, entonces ∂f/∂x = 2xy |
Ortogonalidad
| Símbolo | Nombre | se lee como | Categoría |
|---|

| perpendicular | es perpendicular a | ortogonalidad |
x  y significa: x es perpendicular a y; o, más generalmente, x es ortogonal a y. y significa: x es perpendicular a y; o, más generalmente, x es ortogonal a y. |
Álgebra matricial
| Símbolo | Nombre | se lee como | Categoría |
|---|

| perpendicular | traspuesta | matrices y vectores |
(a,b) con  al lado o a modo de potencia significa que el vector se debe ubicar no de izquierda a derecha, sino de arriba a abajo. En numerosos trabajos de investigación se utiliza esta sintaxis al no poder representar en un documento vectores verticales. al lado o a modo de potencia significa que el vector se debe ubicar no de izquierda a derecha, sino de arriba a abajo. En numerosos trabajos de investigación se utiliza esta sintaxis al no poder representar en un documento vectores verticales. |
Teoría de rejas
| Símbolo | Nombre | se lee como | Categoría |
|---|

| fondo | el elemento fondo | teoría de rejas |
x =  significa: x es el elemento más pequeño. significa: x es el elemento más pequeño. |
 o
o 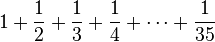 se entiende como suma de fracciones periódicas.
se entiende como suma de fracciones periódicas. se entiende como una matriz de progresión donde los elementos comienzan por la fila y columna de subíndice 1 y terminan en la fila de subíndice 2324, y la columna de subíndice 127.
se entiende como una matriz de progresión donde los elementos comienzan por la fila y columna de subíndice 1 y terminan en la fila de subíndice 2324, y la columna de subíndice 127.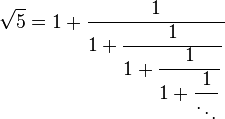 se entiende que la raíz cuadrada de 5 es igual 1 sumado la fracción de 1 sobre la repetición infinita de la misma ecuación.
se entiende que la raíz cuadrada de 5 es igual 1 sumado la fracción de 1 sobre la repetición infinita de la misma ecuación. significa que si se hace seis pedazos uniformes de cuarenta y dos, cada pedazo será de tamaño siete.
significa que si se hace seis pedazos uniformes de cuarenta y dos, cada pedazo será de tamaño siete.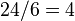
 x
x =1 y
=1 y  x
x =2
=2 y significa: x es perpendicular a y; o, más generalmente, x es ortogonal a y.
y significa: x es perpendicular a y; o, más generalmente, x es ortogonal a y. al lado o a modo de potencia significa que el vector se debe ubicar no de izquierda a derecha, sino de arriba a abajo. En numerosos trabajos de investigación se utiliza esta sintaxis al no poder representar en un documento vectores verticales.
al lado o a modo de potencia significa que el vector se debe ubicar no de izquierda a derecha, sino de arriba a abajo. En numerosos trabajos de investigación se utiliza esta sintaxis al no poder representar en un documento vectores verticales. significa: x es el elemento más pequeño.
significa: x es el elemento más pequeño.


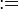

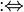

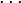







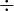
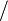












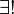
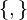
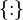





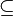




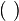
![\left[\ \right]](https://upload.wikimedia.org/math/3/a/6/3a6a4b52a2ccd7ec58002cb495362e16.png)
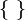










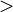

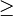

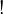

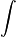
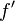

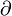
excelente, solo hay que dispersar toda la información en varias paginas para darle otra forma al blog, pues en una sola se ve algo tedioso para los lectores... le falta mas información sobre ud en el perfil recuerde que hay miles de millones de personas que pueden ver su trabajo. otra cosa importante en su breve introducción le falta mas convicción sobre la simbologia matemática...
ResponderEliminarexcelente diseño veo que te esmeraste, pero si; hay demasiada información y eso no se mira bonito xD pero de lo contrario esta muy bien.
ResponderEliminarMuy Bien Nectvin...!! Muy Bien el diseño, tiene mucho información. Pero Te Quedo Bueno Nectvin.
ResponderEliminarMucha información ni la leí toda xD
ResponderEliminarexelente man sólo todo se mira perfecto el fondo pero le metiste demasíada información a una sóla página debiste distribuir la información por páginas lo de más exelente te felicito.
ResponderEliminarExelente Nectvin...
ResponderEliminarMe Gusto Mucho El Diseño....
Solo Una Pequeña Observacion Demasiada
Informacion...
Pero Esta MUY bien...
Super, solo que mucha info. En una sola pagina
ResponderEliminarEsta súper tu blog pero como dicen los demás deberías dividir la información en diferentes paginas
ResponderEliminarMe llega tu blog y a pesar que fue un tema dificil te salio bien
ResponderEliminarsi Tu problema es la informacion que se ve un poco distorcionada y lo demas esta excelente me gusta el diseño que le diste..
ResponderEliminar¡WOW! Muy buen Blog, me gusta bastante el diseñó de la plantilla que usaste. Si, hay mucha información en un sola pagina, y primera vista no dan ganas de leer todo esa informacion, si la dividieras en diferentes páginas seria perfecto.😉
ResponderEliminarjue!! te luciste nectvin... me gusto mucho tu blog tenes buena informacion solo que deberias clasificarla..
ResponderEliminartodo esta muy bien pero le pusiste mucha informacion
ResponderEliminarGracias X sus comentarios chicos! si estoy de acuerdo con lo de la informacion en una sola pagina Tratare de editarlo Bien
ResponderEliminarTodo Bien Me Gusto Tu Encabezado Esta Muy Original!
ResponderEliminarY Solo Divide La Informacion Y Te Quedara Muy Bueno!.
quedo muy bien, nada mas la distribucion de la informacion, pero lo demas esta muy bien.
ResponderEliminarMe gusta el color y todo pero va todo en una sola pagina pero de ahí todo esta súper buen . 😉
ResponderEliminarExelente explicaste bien el tema
ResponderEliminarEstá muy bien explicado, deberías ampliar la información. Saludos, colega. :)
ResponderEliminarMe ha parecido sensacional. Poco espacio y mucha -y explicada- información.
ResponderEliminarLo he leído entero por su sencillez
Me ha parecido sensacional. Poco espacio y mucha -y explicada- información.
ResponderEliminarLo he leído entero por su sencillez
me encanto la respuesta y de como podemos relacionar la matematica con otras materias
ResponderEliminarpues si wy no mms esta mucho
ResponderEliminarBUENA LA INFORMACION
ResponderEliminarGracias por la información me sirvió de mucho☺️🤗😘
ResponderEliminarTe quedo excelente yo me vuelvo loca haciendo todo eso jjj
ResponderEliminarExcelente!!!
ResponderEliminarMuchísimas gracias por compartirlo!!! Me es super util!!!
ResponderEliminar